The paper stating the RUM conjecture was published by a group of Harvard DASLab researchers in 2016. They also have created a more easily digestable RUM conjecture home page with graphics. Yet, in this blog post I try to describe the idea in even simpler terms than that page.
The letters in the RUM conjecture represent Read, Update and Memory. Because this is an academic article, by "Memory" they actually mean "Disk". Mark Callaghan later proposed the CRUM conjecture, where C stands for Cache, in other words.. ehh... Memory. To keep this blog post at a beginner level, I will simply omit any discussion about Memory, Cache and Disk and just focus on Read optimized vs Write optimized database engines.
Read and Write optimized databases
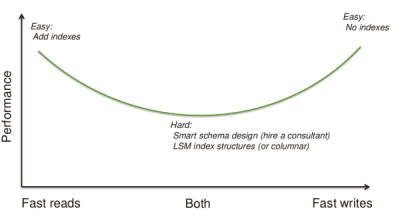
To understand the RUM conjecture, imagine that you are a database consultant doing query optimization for a regular classic relational database. Now, if I told you that I just want the queries to be as fast as possible, then your job is easy: Just add enough indexes so that each query becomes optimal, and you're done. Of course, writes will become terrible slow with 15 indexes, but you didn't have write performance as a requirement.
And if I told you that I want the writes to be really fast and I don't care if queries are slow, then your job is also easy: Just write data into a regular file and toss the database! (See image above for illustration.)
Of course, most applications both read and write to the database and require decent performance for both queries and updates. It is here that we have the hard problems of database tuning and optimization. If you need help, maybe you hire a database consultant to figure out the optimal schema design for you.
RUM conjecture is the same thing for storage engines
The RUM conjecture is about this same problem, but on the storage engine level. When we study different data structures, it turns out some are more read optimized while others are more write optimized.
A B+Tree is the classic index structure used by most databases until the last 10 years or so. Like in most trees, reads can be done in Log(N) time. When there are updates, then the tree must be updated. This means that the work to update each index is done at write time. Since databases typically want to flush updates to disk synchronously at commit time, all of the index maintenance work can be seen in the latency for writes.
A write optimized database engine is a data structure - Cassandra uses Log Structured Merge trees (LSM) - that tries to make writes faster. Since nothing in life is free, the only way we can makes writes faster is to make a trade off: If we try to do less work during the update, it means we have to do more work during the read operations instead. For a write heavy workload this can very well be a good trade off.
The RUM paper uses simple data structures to argue its point. It's not a proof rather the claims are intended to be obvious due to the simplicity. In fact, my example of just using an unsorted text file is also in the RUM paper. You could create such a database using the unix command line tools echo and grep! It turns out this is the most optimal structure for write performance: O(1). (Obviously that is the best case.) Of course, to "query" anything from such a file is rather not efficient: O(N). (The worst case, at least in the universe of meaningful alternatives for this problem.)
B-Trees and LSMs
An LSM data structure is better for reads than a text file and grep, but it's the same idea. Updates are added to a small in-memory data structure called the memtable. (And logged to a file on disk for durability.) This way they are always fast, since updates require no disk access at all (apart from the logging). Periodically this in memory data structure is then written to disk and merged with other data already on disk. But since this is done at a later point in time, this work a) doesn't contribute to the latency experienced by a single update, and b) work for multiple updates can be aggregated and amortized into a single batch of writes. But for reads all this means that there isn't a single big index where we can just look up the record we want to find. Rather multiple versions of a record may exist in several different files. The read must now look into many files, and the memtable too. It will eventually find the record in one of them, but this is much more work and therefore reads can be slower than they would for a classic B+Tree.
So what difference does it make in practice? Below are some benchmark results from a benchmark Mark Callaghan did in 2014. The benchmark is to insert data into a database, with some secondary indexes present, until the database size is about 300GB. Test was done with three different cache sizes:
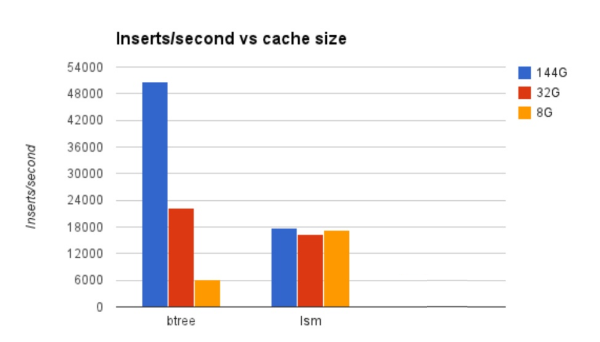
As you can see, with a large cache (blue), when all work in practice fits in RAM, the B-Tree is fast even for writes. (This also is an example of the C=Cache dimension in Mark's CRUM conjecture: If you just add more RAM, then the B-Tree is going to be fast.)
The LSM is a more complicated data structure, so it has to do more work per insert and the throughput is lower. However, if the cache is smaller, then the difference evens out (red) and eventually when the workload is pretty much entirely disk bound the B-Tree is really slow but the LSM engine continues at the same speed it always did!
This is the reason LSM database engines have become popular lately: There is more and more data, and RAM remains expensive.
- Log in to post comments
- 741 views
